
A 5-Step Guide on incorporating Differential Privacy into your Deep Learning models
Using PyTorch and Differential Privacy to classify MNIST digits
7/15/2019
Introduction
By now we all know the benefits of Differential Privacy, how it can protect individual privacy while still providing accurate query results over a large dataset. This post will illustrate how to apply Differential Privacy to the MNIST Digit classification problem and analyze it using a technique called Private Aggregation of Teacher Ensembles (PATE).
Methodology
First, we will divide the private data into N number of sets (in this case, 100) and train a classifier on each of the N datasets. These are called Teacher classifiers. We will then use the teacher classifiers to predict the labels for our public data. For each image in the public dataset, the most predicted label by the N classifiers will be considered as the true label for that image.
Now, using the predictions of the Teacher classifiers as true labels for our public data, we will train a Student classifier which can then be used to classify new unseen images.
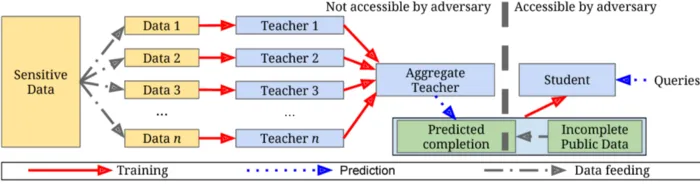
_The MNIST Train data will be considered as private data on which we will train our Teacher models. The Student model obtained by combining the predictions of the teacher models will then be trained on the MNIST Test data (90% of test data will be used to train the model and the remaining 10% will be used to test its accuracy)
Okay, but where does the privacy part come into play?
Deep Learning models have a tendency to overfit the training data. Instead of learning general features, neural networks can learn features of an individual which then can be exploited by an adversary to obtain the individual’s private information.
By not training the Student model directly on the private data, we prevent it from directly learning key individual features of a single person from the dataset. Instead, the generalized features and trends learned by the Teacher models are used to train the Student.
However, there is one small caveat. If the label of an image can be changed by removing the prediction of a single teacher, an adversary can narrow down the search to that model.
To avoid this we add random Laplacian Noise to the predictions of the teacher models before selecting the most predicted label as the true label for the public data. In this way, we add a bit of randomness and skew the final result so that the true label doesn’t easily change by dropping just one teacher.
Implementing Differential Privacy using PyTorch
===============================================
Step 1: Loading the Data
Import the MNIST data from torchvision and define a function to generate the dataloaders.
import torch
from torchvision import datasets, transforms
from torch.utils.data import Subset
# Transform the image to a tensor and normalize it_
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Load the train and test data by using the transform_
train_data = datasets.MNIST(root='data', train=True, download=True, transform=transform)
test_data = datasets.MNIST(root='data', train=False, download=True, transform=transform)num_teachers = 100 # Define the num of teachers_
batch_size = 32 # Teacher batch size_
def get_data_loaders(train_data, num_teachers):
""" Function to create data loaders for the Teacher classifier """
teacher_loaders = []
data_size = len(train_data) // num_teachers
for i in range(data_size):
indices = list(range(i*data_size, (i+1)*data_size))
subset_data = Subset(train_data, indices)
loader = torch.utils.data.DataLoader(subset_data, batch_size=batch_size)
teacher_loaders.append(loader)
return teacher_loaders
teacher_loaders = get_data_loaders(train_data, num_teachers)
Now, generate the student train and test data by splitting the MNIST test set as discussed above.
# Create the public dataset by using 90% of the Test data as train #data and remaining 10% as test data._student_train_data = Subset(test_data, list(range(9000)))
student_test_data = Subset(test_data, list(range(9000, 10000)))
student_train_loader = torch.utils.data.DataLoader(student_train_data, batch_size=batch_size)
student_test_loader = torch.utils.data.DataLoader(student_test_data, batch_size=batch_size)
Step 2: Defining and Training the Teacher models
Define a simple CNN to classify the MNIST digits.
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
class Classifier(nn.Module):
""" A Simple Feed Forward Neural Network.
_A CNN can also be used for this problem_
"""
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
def forward(self, x):
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
x = self.fc2(x)
return F.log_softmax(x)
Now define the train and predict functions
def train(model, trainloader, criterion, optimizer, epochs=10):
""" This function trains a single Classifier model """
running_loss = 0
for e in range(epochs):
model.train()
for images, labels in trainloader:
optimizer.zero_grad()
output = model.forward(images)
loss = criterion(output, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()def predict(model, dataloader):
""" This function predicts labels for a dataset_
_given the model and dataloader as inputs.
"""
outputs = torch.zeros(0, dtype=torch.long)
model.eval()
for images, labels in dataloader:
output = model.forward(images)
ps = torch.argmax(torch.exp(output), dim=1)
outputs = torch.cat((outputs, ps))
return outputsdef train_models(num_teachers):
""" Trains *num_teacher* models (num_teachers being the number of teacher classifiers) """
models = []
for i in range(num_teachers):
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
train(model, teacher_loaders[i], criterion, optimizer)
models.append(model)
return modelsmodels = train_models(num_teachers)
Step 3: Generate the Aggregated Teacher and Student labels by combining the predictions of the Teacher models.
Now, we need to choose the epsilon value for which we first define the formal definition of Differential Privacy
This definition does not create differential privacy, instead, it is a measure of how much privacy is afforded by a query M. Specifically, it’s a comparison between running the query M on a database (x) and a parallel database (y). As you remember, parallel databases are defined to be the same as a full database (x) with one entry/person removed.
Thus, this definition says that FOR ALL parallel databases, the maximum distance between a query on database (x) and the same query on database (y) will be e^epsilon, but that occasionally this constraint won’t hold with probability delta. Thus, this theorem is called “epsilon-delta” differential privacy.
How much noise should we add?
The amount of noise necessary to add to the output of a query is a function of four things:
- the type of noise (Gaussian/Laplacian)
- the sensitivity of the query/function
- the desired epsilon (ε)
- the desired delta (δ)
Thus, for each type of noise we’re adding, we have a different way of calculating how much to add as a function of sensitivity, epsilon, and delta. We’re going to focus on Laplacian noise.
Laplacian noise is increased/decreased according to a “scale” parameter b. We choose “b” based on the following formula.
b = sensitivity(query) / epsilon
In other words, if we set b to be this value, then we know that we will have a privacy leakage of < = epsilon. Furthermore, the nice thing about Laplace is that it guarantees this with delta == 0. There are some tunings where we can have very low epsilon where delta is non-zero, but we’ll ignore them for now.
import numpy as np
epsilon = 0.2def aggregated_teacher(models, dataloader, epsilon):
""" Take predictions from individual teacher model and_
_creates the true labels for the student after adding_
_laplacian noise to them_
"""
preds = torch.torch.zeros((len(models), 9000), dtype=torch.long)
for i, model in enumerate(models):
results = predict(model, dataloader)
preds[i] = results
labels = np.array([]).astype(int)
for image_preds in np.transpose(preds):
label_counts = np.bincount(image_preds, minlength=10)
beta = 1 / epsilon
for i in range(len(label_counts)):
label_counts[i] += np.random.laplace(0, beta, 1)
new_label = np.argmax(label_counts)
labels = np.append(labels, new_label)
return preds.numpy(), labelsteacher_models = models
preds, student_labels = aggregated_teacher(teacher_models, student_train_loader, epsilon)
Step 4: Create the Student model and train it using the labels generated in step 3.
def student_loader(student_train_loader, labels):
for i, (data, ) in enumerate(iter(student_train_loader)):
yield data, torch.from_numpy(labels[i*len(data): (i+1)*len(data)])student_model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(student_model.parameters(), lr=0.003)
epochs = 10
steps = 0
running_loss = 0
for e in range(epochs):
student_model.train()
train_loader = student_loader(student_train_loader, student_labels)
for images, labels in train_loader:
steps += 1
optimizer.zero_grad()
output = student_model.forward(images)
loss = criterion(output, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if steps % 50 == 0:
test_loss = 0
accuracy = 0
student_model.eval()
with torch.no_grad():
for images, labels in student_test_loader:
log_ps = student_model(images)
test_loss += criterion(log_ps, labels).item()
# Accuracy_
ps = torch.exp(log_ps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor))
student_model.train()
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Training Loss: {:.3f}.. ".format(running_loss/len(student_train_loader)),
"Test Loss: {:.3f}.. ".format(test_loss/len(student_test_loader)),
"Test Accuracy: {:.3f}".format(accuracy/len(student_test_loader)))
running_loss = 0
Here’s a snippet of the training loss and accuracy achieved.
Epoch: 9/10.. Training Loss: 0.035.. Test Loss: 0.206.. Test Accuracy: 0.941
Epoch: 9/10.. Training Loss: 0.034.. Test Loss: 0.196.. Test Accuracy: 0.949
Epoch: 10/10.. Training Loss: 0.048.. Test Loss: 0.204.. Test Accuracy: 0.943
Epoch: 10/10.. Training Loss: 0.046.. Test Loss: 0.203.. Test Accuracy: 0.943
Epoch: 10/10.. Training Loss: 0.045.. Test Loss: 0.203.. Test Accuracy: 0.945
Epoch: 10/10.. Training Loss: 0.049.. Test Loss: 0.207.. Test Accuracy: 0.946
Epoch: 10/10.. Training Loss: 0.032.. Test Loss: 0.228.. Test Accuracy: 0.941
Epoch: 10/10.. Training Loss: 0.030.. Test Loss: 0.252.. Test Accuracy: 0.939
Step 5: Let’s Perform PATE Analysis on the student labels generated by the Aggregated Teacher
from syft.frameworks.torch.differential_privacy import pate
data_dep_eps, data_ind_eps = pate.perform_analysis(teacher_preds=preds, indices=student_labels, noise_eps=epsilon, delta=1e-5)
print("Data Independent Epsilon:", data_ind_eps)
print("Data Dependent Epsilon:", data_dep_eps)
Output:
Data Independent Epsilon: 1451.5129254649705
Data Dependent Epsilon: 4.34002697554237
The pate.perform_analysis method returns two values - a data-independent epsilon and a data-dependent epsilon. The data-dependent epsilon is the epsilon value obtained by looking at how much the teachers agree with each other. In a way, the PATE analysis rewards the user for building teacher models which agree with each other because it becomes harder to leak information and track individual information.
Conclusion
Using the Student-Teacher architecture guided by the PATE analysis method is a great way to introduce Differential Privacy to your deep learning models. However, Differential Privacy is still in its early stage and as more research in the space occurs more sophisticated methods will be developed to reduce the privacy-accuracy tradeoff and the downside that differential privacy only really performs well on large datasets.
References
[1] Dwork, C. and Roth, A. The algorithmic foundations of differential privacy (2014), Foundations and Trends® in Theoretical Computer Science, 9(3–4), pp.211–407.
[2] Abadi, Martin, et al, Deep learning with differential privacy (2016), Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. ACM, 2016.
[3] Figure 1, Photo by Farzad Nazifi on Unsplash
[4] Figure 2, Nicolas Papernot, et al, Scalable Private Learning with PATE(2018), Published as a conference paper at ICLR 2018